Chemische Formeln als Symbolsprache der Chemie sind nicht nur ein unverzichtbarer Bestandteil der Fachwissenschaft, ohne deren Kenntnis und Verständnis ist in der Schule auch in der Sekundarstufe I auf die Dauer kein sinnvoller Chemieunterricht möglich. So bedarf die Einführung chemischer Formeln an sich keiner weiteren Legitimation, lediglich über den sinnvollsten Zeitpunkt gibt es unterschiedliche Ansichten.
Ursache dafür ist die Tatsache, dass für Schülerinnen und Schüler in der Sekundarstufe I die chemischen Formeln und chemischen Gleichungen häufig zu den schwierigen und nicht verstandenen Sachverhalten gehören, die zu Aversionen gegenüber dem Unterrichtsfach Chemie führen. Es ist deshalb besonders wichtig, diese Inhalte durch- und einsichtig zu erarbeiten und darzustellen, um letztlich durch Verständnis und Anwendung auf weitere Probleme Vorbehalte abzubauen und Erfolgserlebnisse zu vermitteln.
Für den Weg zur chemischen Formel wurden in der Vergangenheit verschiedene Vorschläge gemacht, so z.B. über die so genannten Wertigkeiten oder über das Auszählen der Atomzahlenverhältnisse in räumlichen Anschauungsmodellen. Andere Vorschläge zielen darauf hin, nur die Atomsymbole einzuführen und in stark vereinfachten Formeln nur die beteiligten Atomarten anzugeben. Eingewandt wird gegen diese Vereinfachung, dass sie in der Wissenschaft Chemie keinen Platz hat und dass die Schülerinnen und Schüler das Bedürfnis haben, die "richtigen" Formeln zu kennen und zu verstehen.
Der wohl am häufigsten auch in Schulbüchern vorgeschlagene Weg entspricht in etwa dem historischen zu chemischen Formeln. Ausgehend von dem Gesetz der Erhaltung der Masse wird zunächst das der konstanten Proportionen erarbeitet oder (gelegentlich fragwürdig) am Beispiel der Reaktion von Eisen mit Schwefel demonstriert. Daraus sollen dann möglichst die Schülerinnen und Schüler selbst scheinbar zwingend und logisch die Daltonsche Atomtheorie ableiten.
Um in der Folge chemische Formeln zu ermitteln, werden zunächst die Atommassen vorgegeben, dann wird (möglichst experimentell) ein Massenverhältnis zweier Atomarten in einer Verbindung ermittelt. Dieses muss anschließend wiederum mit dem Atommassenverhältnis der an der Verbindung beteiligten Atome korreliert werden.
Zunächst einmal ist an dieser Stelle für die Schülerinnen und Schüler gar nicht einsichtig, warum in chemischen Formeln nicht die gerade erst mit Mühe ermittelten Massenverhältnisse zum Ausdruck kommen sollen, sondern noch wieder Atomzahlenverhältnisse berechnet werden müssen.
Weiterhin ist gegen diese Vorgehensweise einzuwenden, dass zwar die Ermittlung der Massenverhältnisse noch konkret und anschaulich durchzuführen ist. Die daraus in einem recht aufwendigen Verfahren zu berechnenden Atomzahlenverhältnisse beinhalten aber neben dem Wechsel in die Unanschaulichkeit noch einen weiteren Aspekt, der zu Verständnisschwierigkeiten bei den Schülerinnen und Schülern führen kann: In gleichen Massen verschiedener Stoffe sind auch unterschiedlich viele Atome enthalten. Das erfordert nicht nur die Vorstellung von unterschiedlichen Massen der einzelnen Atomarten, sondern auch von deren Größe und deren Abstand zueinander. Dieses ist dem Lehrenden klar, bei den Lernenden ist eine entsprechende Kenntnis jedoch nicht ohne weiteres vorauszusetzen. Sie wissen allenfalls, dass gleiche Volumina von Feststoffen unterschiedliche Massen haben.
Will man also die Schülerinnen und Schüler auf dem klassischen Weg zur chemischen Formel führen, muss ihnen nicht nur die mathematisch-formale Umrechnung vermittelt werden, sie müssen auch noch erkennen, dass massengleiche Stoffportionen unterschiedlich viele Atome enthalten. Dieser Weg ist sehr komplex und erfordert für das Verständnis bzw. das Nachvollziehen ein hohes Maß an "geistiger Kraft" sowie die Fähigkeit zu formal-operationalem Denken. Da zu letzterem aber viele Schülerinnen und Schüler auch in der 10. Klasse offensichtlich noch nicht in der Lage sind, wird deutlich, warum es bei dieser Thematik häufig zu Verständnisschwierigkeiten kommt, die letztlich zu Aversionen führen.
Eine sich daraus ergebende Konsequenz ist die bereits genannte Diskussion um den richtigen Zeitpunkt zur Einführung chemischer Formeln oder um vereinfachte Schreibweisen. Teilt man aber die gegen den letztgenannten Punkt geäußerten Einwände und gelangt zu der Auffassung, dass Schülerinnen und Schüler, die die Schule nach der 10. Klasse verlassen, auch Grundkenntnisse von chemischen Formeln besitzen sollten, so muss über den Weg ihrer Einführung neu nachgedacht werden.
Wir schlagen deshalb folgende Vorgehensweise vor:

Den Ausgangspunkt zum Übergang von Wortgleichungen zu Summenformeln und chemischen Reaktionsgleichungen in der Formelschreibweise bildet die Daltonsche Atomtheorie, die Atome erhalten letztlich quasi als Etiketten die Abkürzungen der Elementnamen. Nun ist in der Daltonschen Theorie der wirklich neue und revolutionierende Gedanke enthalten, dass in chemischen Verbindungen die Atome in ganz bestimmten, einfachen Zahlenverhältnissen zusammentreten. Kann man also die bisher für die Schülerinnen und Schüler gewohnten Wortgleichungen durch einfache Symbolgleichungen ersetzen? Kann man statt der Wortgleichung

         Magnesium + Sauerstoff reagiert zu Magnesiumoxid

auch

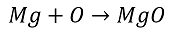
schreiben?

Schon der Vergleich der Namen der beiden bekannten Stoffe Magnesiumoxid und Kohlenstoffdioxid macht deutlich, dass die Atome in Verbindungen nicht immer unbedingt im Verhältnis 1 : 1 zueinander stehen. Leider sind aber die Atome so klein, dass man nicht abzählen kann, in welchem Verhältnis sie miteinander reagieren. Deshalb muss man sich eine andere Möglichkeit einfallen lassen, um das herauszufinden.
An dieser Stelle können die Schülerinnen und Schüler in der Regel nicht alleine weiterkommen, sie sind auf Hilfestellungen angewiesen.
Um das Problem lösen zu können, werden sie aufgefordert, eine Aufgabe zu bearbeiten, die im Moment nicht nahe liegend erscheint: Sie erhalten in mehreren Gruppen jeweils eine geschlossenen Packung mit Würfelzucker und ein einzelnes Stückchen Zucker. Damit sollen sie dann herausfinden, wie viel Stückchen sich in der Packung befinden, ohne diese zu öffnen.
Im allgemeinen kommen sie sehr schnell auf zwei Lösungsansätze: Entweder messen sie die Kantenlängen des Stückchens und der Packung und bestimmen über das Volumen die Anzahl, oder sie bitten um eine Waage, bestimmen die Massen des einen Stückchens und der Packung und ermitteln durch Quotientenbildung die Stückzahl. Beide Vorgehensweisen führen meistens zu dem richtigen Ergebnis, wie man im Anschluss durch Öffnung der Packung und durch Nachzählen feststellen kann.
Will man dieses Modellexperiment auf die Bestimmung der Anzahl von Atomen in Stoffportionen übertragen, so wird schnell klar, dass nur der zweite Lösungsweg dafür geeignet scheint, da man Atome und unsymmetrische Stoffportionen schlecht vermessen kann. Fordert man nun die Schülerinnen und Schüler auf, einmal formal auszudrücken, wie sie auf die Anzahl gekommen sind, so werden sie leicht folgenden Zusammenhang darstellen können: 

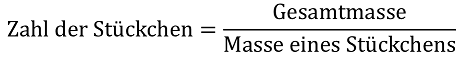
Analog müsste man die Anzahl der Atome in einer Stoffportion herausfinden können, indem man formuliert:

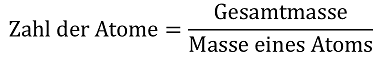
Die Masse einzelner Atome wird man vorgeben müssen, da ein Nachvollziehen von Methoden zur Bestimmung von Atommassen in der Sekundarstufe I nicht leistbar ist. Es ergibt sich lediglich das Problem, dass zur Berechnung der Anzahl von Atomen entweder die wägbare Masseneinheit Gramm in die Atommasseneinheit u umgerechnet werden muss oder umgekehrt. Es fehlt ein Umrechnungsfaktor zwischen den beiden Größen, der sich auf die folgende Weise auch für Schülerinnen und Schüler der Sekundarstufe I veranschaulichen lässt:

1 g = 1000 mg = 10³ mg
1 g = 1.000.000 µg = 10⁶ µg
1 g = 1.000.000.000 ng = 10⁹ ng
...
1 g = 602.000.000.000.000.000.000.000 u = 6,02 · 10²³ u

Der Umrechnungsfaktor bleibt im folgenden immer insgesamt erhalten und wird später einfach durch die Abkürzung mol ersetzt, also sind z.B.

2 g = 2 · 6,02 · 10²³ u
3 g = 3 · 6,02 · 10²³ u

bzw.

2 g = 2 mol u
3 g = 3 mol u
usw.

Damit lässt sich problemlos bei Feststoffen oder auch bei Flüssigkeiten die Zahl der Atome bzw. kleinsten Teilchen berechnen, z.B. bei einem Eisennagel mit einer Masse von 2,8 g:

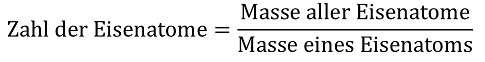
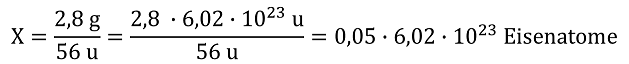
bzw. X = 0,05 mol Eisenatome

Diese Art der Vorgehensweise zur Ermittlung von Teilchenzahlen bietet neben der deutlich geringeren Komplexität für die Schülerinnen und Schüler zwei entscheidende Vorteile gegenüber dem klassischen Weg:
Zum ersten ermöglicht sie ihnen durch den vorgeschalteten "Zuckerstückchen-Versuch" anhand konkret-anschaulicher "Teilchen", selbständig eine Lösung und vor allem einen Lösungsweg zu finden, wie man die Anzahl von Teilchen bestimmen kann, ohne diese zu sehen oder abzuzählen. Der Übergang auf die "unanschaulichen" Atome wird dadurch wesentlich erleichtert, da im Grunde genommen nur die Zuckerstückchen gegen Atome und die Einheit Gramm gegen 6,02 · 10²³ u ausgetauscht werden.
Zum zweiten verliert auf diese Weise der Molbegriff den Charakter des "Schwierigen" und "Unanschaulichen". Wie die Abkürzung "Dutzend" für zwölf wird der Begriff "mol" als eine Abkürzung für die Zahl 6,02 · 10²³ eingeführt.

Zum weiteren Unterrichtsgang über die Bestimmung der Teilchenzahlen in Gasen, den Satz von Avogadro und die Ermittlung von Summenformeln einiger Oxide, die Einführung des Redox- Systems CO₂/CO und Probleme bei der Reaktion von Magnesium mit Kohlenstoffdioxid sind in der folgenden Literatur zu finden.